Link to the GitHub Repo: AI Snake Repo

artificial-intelligence-snake

AI is trained to play the game of snake using a shallow neural net (2 hidden layers) and the genetic algorithm.

What are the red and white squares? (click to show)
The snake receives 14 input parameters: The red and white squares are placed at the 8 obstructions that the snake sees in the third bullet point. The square is white if the obstruction is the snake's body and red if the obstruction is the wall. This means that the snake typically does not know where the majority of it's tail is.

What is the count down?
The count down is for the snakes energy. Every space that the snake moves costs the snake one unit of energy and everytime the snake eats food it gains 100 units of energy and grows one unit longer. When the snake is low on energy (less than 200) the meter gradually turns from green to dark red.

Generation 1 versus Generation 343

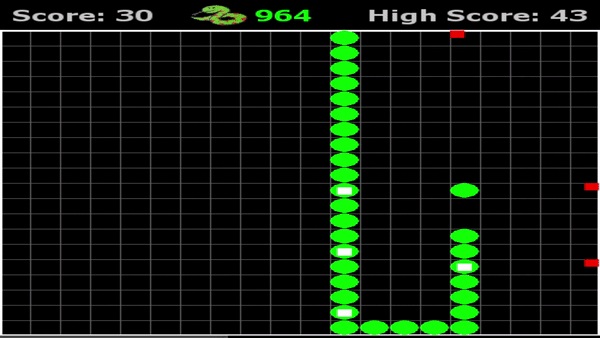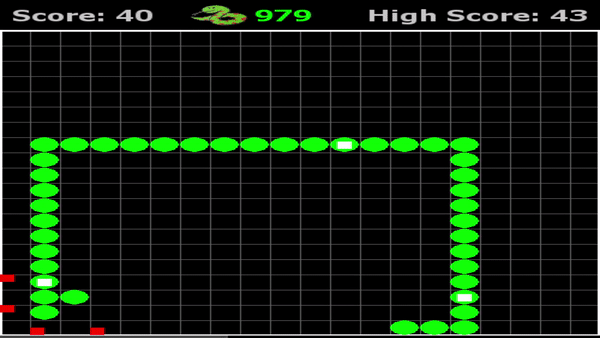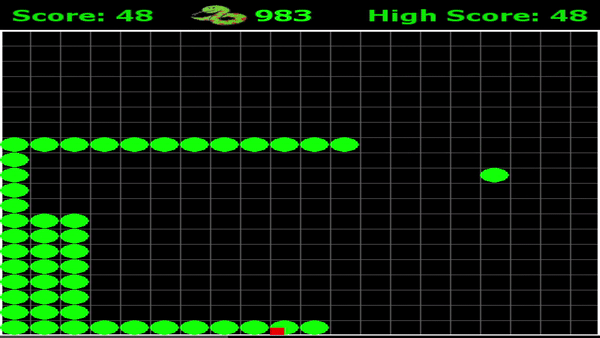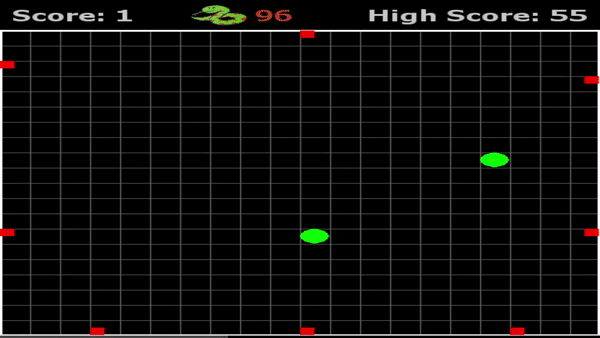
Can you defeat AI snake?

Try the playing JavaScript version here: AI Snake JavaScript Version

Please excuse my JavaScript, converting this project from python to JavaScript was my first experience with the language.

Learning Timelapse:

Click on the generation name to show / hide progress.
Each generation shows the best preforming neural net of 500 snakes from that generation.

Generation 1: likes to run into walls
Generation 5: learns that cycles prolong it's life
Generation 20: getting food has a larger reward than a long life, starts to go towards food
Generation 76: ... not much progress since gen 20
Generation 85: First signs of a real strategy! Loops towards food.
Generation 91
Generation 131
Generation 171: A cyclic strategy that avoids walls and targets food emerges!
Generation 231
Generation 271: Hug the wall strategy. Only leaves for food.
Generation 300
Generation 318
Generation 343: Balances survival and desire for food by prioritizing obstacle avoidance when a direct path to the food would result in game over and prioritizing food when there is a clear path.

History

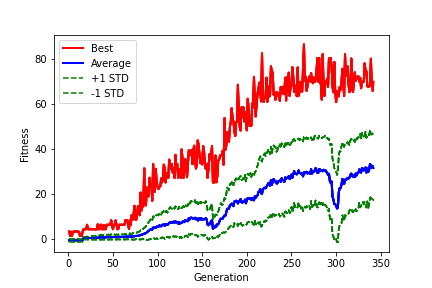
A fitness function, described below was used to judge how well each of the 500 snakes in each generation performed. The best performing snake's score from each generation is shown in the red line. While the average fitness score of a generation is shown as the blue line. The green lines show ± 1 standard deviation from the average.

Notice at generations 160 and 290 there are sharp drops in the average fitness score. At these points the average model's fitness score appeared to be improving at an asymptotic rate. So the mutation rate was increased to somewhere between 0.05 and 0.1 for a few generations in an effort to shake up the models. After which the mutation rate was decreased to between 0.01 and 0.03. This "shaking up" resulted in short but signifcant periods of rapid improvement.

Overview

The objective of snake is to eat as much food as possible without dying.
The snake dies if it bites its tail or if it goes out of bounds.
Every time the snake finds food, it grows in length by 1.
Here a new factor is imposed, hunger.
The snake must find food within food_energy steps or else it will starve.
Every time the snake eats food it gains food_energy steps up to a cap of 999.

Usage

ga_snake_playback.py (click to show)
Loads the last N trained models.
Plays snake using the trained model as shown in the above GIFs.
left-arrow key: snake uses the model from the previous generation
right-arrow key: snake uses the model from the next generation
up-arrow key: speeds the game up
down-arrow key: slows the game down

ga_snake_train.py (click to show)
Runs a population of 500 snakes per generation. Each snake will be scored based on how many steps it took and how much food it found. The top survival_fraction (10%) of snakes are allowed to breed. Breeding means their neural network weights will be crossed with other snakes from the pool to create the next generation of snakes.
The nerural network weights for the entire last generation of snakes is always saved in "./ga_snake_history/checkpoint_weights" so that the training can be stopped after a given generation and resumed with a different settings if desired.

Settings

settings_playback.py (click to show)
grid_size: controls the columns and rows in the grid
food_energy: energy gained by the snake for finding food
nn_shape: [number_of_input_nodes, *hidden_layer_nodes, number_of_output_nodes]
activation_functions: activation functions used for neural net hidden and output layers
watch: True will display the game, False will hide the game
autoplay: True will cycle through all loaded generations automatically
clock_speed: Initial ms delay between frames can be changed in game with up/down keys
colorful: If True snake will take the color of its rainbow food
play_top_n_gen: How many generations to load (0 will load all generations)
basic_instincts: Hardcoded rules imposed on top of neural net (looks 1 step ahead)

settings_training.py (click to show)
grid_size: controls the columns and rows in the grid
food_energy: energy gained by the snake for finding food
population: number of snakes per generation
generations: how many generations to run for before stopping
fitness_threshold: if any snake receives this score stop running
mutation_rate: Probability of any given gene being mutated
mutation_type: gaussian adds value from gaussian dist. to mutated weights while uniform replaces mutated weights with a random value from a uniform dist.
mutation_range: range of unifrom dist. values
survival_fraction: the top survival_fraction of snakes will survive and be used to breed the next generation
nn_shape: [number_of_input_nodes, *hidden_layer_nodes, number_of_output_nodes]
activation_functions: activation functions used for neural net hidden and output layers
initial_config: If True, continues training from last save point. Otherwise starts over from gen 1. watch: True will display the game, False will hide the game

Try it yourself.

If you do not already have TensorFlow installed, you can play against the ai-snake here:
AI Snake JavaScript Version

Genetic algorithm process

I will discuss this section in more detail in the future, but for now here is the process in a nut shell. (click to show)
Each snake is an agent. And the agent's DNA consists of 422 genes. Where each gene is a floating point number that represents either a connection weight or a bias weight in the neural net.
422 comes from the shape of the neural net, 18 inputs, 14 hidden_layer_1 nodes, 8 hidden_layer_2 nodes, and 4 output nodes.
This gives rise to 14 + 8 + 4 bias weights, one per node for each layer after the input layer.
And (18 x 14) + (14 x 8) + (8 x 4) connection weights to fully connect the input layer to hidden 1, hidden 1 to hidden 2, and hidden 2 to the output layer.
The neural net treats these weights as 6 matrices of shapes (18 x 14), ..., (1 x 8), (1 x 4).
However for the genetic algorithm it is easier for us to think of the nodes as a flattened array of dimensions (1 x 422).

Aside
In this project I actually did flatten the array to work with it and then returned it to it's original shape. In hind sight (returning to this project several months wiser) I realize it would be more efficient to perform the genetic algorithm steps without flattening the arrays. A simple improvement for next time...

The first generation 500 agents (snakes all with randomly generated weights) will all play one game of snake.

For every step an agent takes, they get 0.01 point, for every piece of food they get they earn 2 points, and they receive a small penalty for hitting the wall (perhaps -0.5 points).

Lesson Learned (rewards)
In the beginning when most of the snakes are just running straight into the wall, they would have learned faster if I did not reward them for getting food. At this stage, even the wall chargers may get lucky and find food. Then they will get 2 points and look like a strong neural net (which they are not). So when they breed they will bring down the next generation. If I did this again, I would wait until the snakes starve from running around before adding the food reward bonus.

After all 500 agents have run, they are sorted by their fitness function (which is the total reward they earned). Only the top 10% of the snakes are allowed to live and breed.

Live means the top 10% of agents will appear in the next generation unchanged. Breed means we randomly select 2 of the surving agents and build a new agent by randomly gene[i] from parent1[i] or parent2[i] where i is the ith genome. This process is called crossover.

Then randomly mutate 0.03% of the new agent's weights where a mutation consists of adding a random value from a gaussian distribution to the weight.

The mutation rate can be set anywhere from 0 to 0.1.

Lesson Learned (mutation rate)
Having a high mutation rate can be very damaging to a fine tuned neural network. However, it can also be the kickstart that the network needs. If you are seeing asymptotic growth in you fitness function from generation to generation and you think your model is capable of performing better. First, save a backup of the current state of your model's weights. Then, crank up the mutation rate, run for a few generations, then bring the mutation rate back down. This will shake up some of the weights and may result in a significant increase in overall peformance as seen around generation 160 in this project.

You might also consider changing the rewards to overcome whatever challenge is currently holding your model back. For example here, one of the major problems currently is the snake entering a closed space smaller than the length of the snake - almost certain death. Adding a negative reward to punish this behavior may help push the model to another level.

After mutation, the next generation of agents is ready to be tested, and the cycle continues.

This process of selecting the most fit agents, performing cross-over on their genes, and mutating a random subset of the genes will gradually tune the neural networks weights to create a fit agent.

I will not discuss all of the dangers and short-comings of the genetic algorithm here, but I will point out one that is easily observable in the above plot. And that is the risk of getting caught in a local maxima. Truncating the fitness vs generation plot at 160, 270, or 343 generations, it looks like the model is approaching it's maximum, but there's no guarantee that a substantially better combination of weights for the model does not exist.